In this chunk we will continue on from the last by using the vertex function to create shapes. However, this time we will extend the animation to three-dimensional shapes. What we are attempting to draw is shown in figure 48.1 below
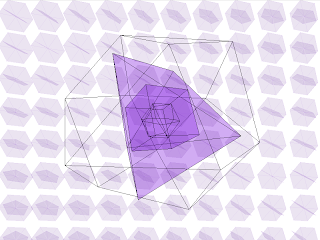
Figure 48.1 The final animation
This looks extraordinarily complex, so we will break it down into parts and explain how each part is done. As we have already drawn hexagons in the previous chunk, we will start with those, but we will alter the code so we can reuse it to create other shapes.
Each vertex in a polygon can be calculated using a formula related to the number of sides. Most polygons (that is 2D shapes) can be drawn using the same formula, so we will be able to reuse it to draw polygons with different numbers of sides. Using trigonometric functions, which we will describe in more detail later in the book, we can calculate each vertex by
x-coordinate = (coordinate + edge size * cos(current side index * 2 * PI / sides));
y-coordinate = (coordinate + edge size * sin(current side index * 2 * PI / sides));
We can use this to create a generic function for creating polygons
/**
* Draw a 2D polygon with the given number of sides and size
* @param sides the number of sides
* @param size the size of one edge
*/
void draw2DPolygon(int sides, int size) {
// starting coordinates
int x = 0;
int y = 0;
// draw the polygon
beginShape();
// loop for the number of sides + 1 (so we join up the last side to the starting vertex)
for (int i = 0; i <= sides; i++) {
// work out the coordinates of the vertex
float xCoord = (x + size * cos(i * 2 * PI / sides));
float yCoord = (y + size * sin(i * 2 * PI / sides));
// plot the vertex
vertex(xCoord, yCoord);
}
endShape();
}
The centre point of the hexagon can be calculated in a similar way and the lines drawn from each vertex to the centre. Although this initially seems like it is more complicated than the method seen in chunk 47, it is a much more generic way of creating the hexagon that means we can use it to create other polygons. This means we can easily draw a smaller pentagon simply by calling our function with different arguments. If we add a loop, similar to how we implemented the previous 'hexagon wave', we can create our background of rotating polygons. The code now looks like the below
int hexagonSize = 40;
int pentagonSize = 30;
void setup() {
size(800, 600, P3D);
}
void draw() {
// define rotation direction variables
float clockwiseDirection = frameCount * PI;
float antiClockwiseDirection = frameCount * -PI;
background(255);
// loop over the hieght of the screen
for (int i = hexagonSize; i < height + hexagonSize; i = i + (hexagonSize * 2)) {
// loop over the width of the screen
for (int j = hexagonSize; j < width; j = j + (hexagonSize * 2)) {
pushMatrix();
translate(j, i, 0);
// hexagon
rotateZ(antiClockwiseDirection / 150);
rotateX(antiClockwiseDirection / 150);
rotateY(antiClockwiseDirection / 150);
draw2DPolygon(6, hexagonSize);
// pentagon
rotateZ(clockwiseDirection / 255);
rotateX(clockwiseDirection / 255);
rotateY(clockwiseDirection / 255);
draw2DPolygon(5, pentagonSize);
popMatrix();
}
}
}
/**
* Draw a 2D polygon with the given number of sides and size
* @param sides the number of sides
* @param size the size of one edge
*/
void draw2DPolygon(int sides, int size) {
// fill colour
fill(85, 26, 139, 30);
// line colour
stroke(138, 43, 226, 20);
// starting coordinates
int x = 0;
int y = 0;
// centre coordinates
float centreX = 0;
float centreY = 0;
// work out the centre coordinates using the coordinates of each vertex
for (int i = 0; i < sides; i++) {
// work out the coordinates
float xCoord = (x + size * cos(i * 2 * PI / sides));
float yCoord = (y + size * sin(i * 2 * PI / sides));
// add them all together
centreX += xCoord;
centreY += yCoord;
}
// calculate the centre coordinates
centreX = (centreX / sides) * -1;
centreY = (centreY / sides) * -1;
// draw the polygon
beginShape();
// loop for the number of sides + 1 (so we join up the last side to the starting vertex)
for (int i = 0; i <= sides; i++) {
// work out the coordinates of the vertex
float xCoord = (centreX + size * cos(i * 2 * PI / sides));
float yCoord = (centreY + size * sin(i * 2 * PI / sides));
// plot the vertex
vertex(xCoord, yCoord);
}
endShape();
// draw the internal lines
// loop for the number of sides
for (int i = 0; i < sides; i++) {
// work out the coordinates
float xCoord = (centreX + size * cos(i * 2 * PI / sides));
float yCoord = (centreY + size * sin(i * 2 * PI / sides));
// plot a line from the coordinate to the centre coordinates
line(xCoord, yCoord, centreX, centreY);
}
// reset the stroke colour to black
stroke(0);
}

Figure 48.2 Background of rotating hexagons and pentagons
Now we can look at drawing the 3D shapes. Processing already has functions for some 3D shapes such as cubes and spheres, so we can utilise those for certain shapes. However, if we want a complicated shape, we will need to draw it ourselves using vertices, as we did with the 2D shapes. This time, though, we also need to specify three coordinates for each vertex to plot it in three-dimensions. Processing's vertex function can have 2 or 3 arguments, so we will be using the 3 arguments required for 3D in the form
vertex(x, y, z);
The shape we are going to draw is a cuboctahedron – a 24-sided polyhedron (a 3D shape made up of polygons) with faces made up of 8 triangles and 6 squares, as shown in figure 48.3
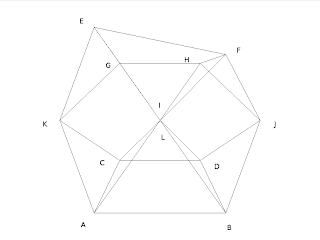
Figure 48.3 Cuboctahedron with vertices marked
In order to create some code that is readable, we will define each vertex in terms of the letters shown in figure 48.3. The simplest way to define a reusable shape is to create a class that defines how the shape is drawn. However, this is covered later in the book, so for now we will use an array and a switch statement – an array to define which points are drawn in which order, and a switch statement to draw the vertex in each element of the array.
The reason we are defining an array is because we need to draw the shape by drawing from one vertex to another – a little like trying to draw without taking your pen off the paper. This means that we end up drawing some of the lines more than once in order to reach the next vertex. The order we have determined, using the labelled points above, is:
A,I,E,K,A,B,J,F,I,B,D,L,H,J,D,C,K,G,L,C,A,I,E,G,H,F,E

No comments:
Post a Comment